En algunas ocasiones nos encontraremos arboles o edificios que nos haran dudar si nos va a librar la antena
os explico dos metodos el Sencillo (Mas practico) y el Matematico
El metodo sencillo para españa
Para satelites distantes mas o menos 30º del Sur geometrico (180º) es decir entre 150ºE y 210ºW nos debemos de separar la altura del objeto multiplicado por 1,8 desde la base donde queremos ubicar nuestra antena.
Si desconocemos la altura del obstaculo podemos utilizar el metodo de las sombras el cual es sencillo y efectivo:
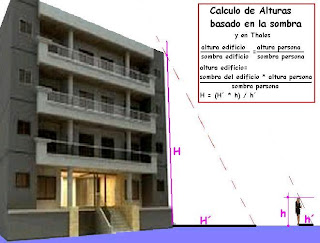
Este calculo, se lo debemos a thales, quien una tarde de verano,se recosto a la sombra de la piramide mayor de Egipto, despues de almorzar un rico asado con cueros y acompañado de una damajuana de 5 litros de vino tinto, de repente mira la sombra y en ese momento fue que le vino la inspiracion, sugiriendole al Rey Amasis que empleara este metodo de la sombra para medir la altura de las famosas piramides. De esa epoca tan antigua, se conoce pues, el metodo para medir la altura de grandes edificios, arboles o montañas y la tradicion de la damajuana de vino tinto para calmar la sed del desierto.
Thales descubrio que existe una relacion de igualdad entre la altura de dos objetos y sus respectivas sombras. Tal como esta en la formula, de esta igualdad podemos obtener el valor de la altura de una de ellas, la cual nos es desconocida.
Sea el caso de un edificio de departamentos que tenemos frente a nuestra casa y deseamos saber su altura para despues saber donde ubicar nuestra antena para apuntar libre de obstaculos.
A eso de las 3 o 4 de la tarde, salimos a la vereda y medimos la sombra del edificio. luego, inmediatamente, nos ponemos firmes y pedimos a un ayudante que mida nuestra sombra. con estos dos datos y conociendo nuestra altura, vamos a poder calcular la altura del edificio.
aplicamos la formulita:
altura de la persona: 1.8 metros
sombra de la persona: 2.7 metros
sombra del edificio.: 20 metros
calculamos H = 20 * 1.8 / 2.7 = 13.33 mts que es la altura del edificio de enfrente. luego, con este dato podemos calcular a que altura colocar nuestra antena para evitar interferencias,etc
Ahora el metodo matematico
Cuando tenemos algun obstaculo delante de la antena, podemos facilmente saber cual sera el angulo de elevacion minimo que podremos apuntar con ella, simplemente haciendo unos calculos.
Para ello emplearemos el conocido teorema de pitagoras y el del seno. el primero es para calcular la hipotenusa del triangulo ABC y luego poder aplicar el teorema del seno y calcular el angulo beta, que es el que nos interesa. como lo hacemos ?, veamos un ejemplo practico:
CASO DE UN MURO CERCANO A LA ANTENA PARABOLICA:
tenemos un muro de ladrillo de 1.50 metros de altura. luego vamos a instalar nuestra antena a una distancia de 1.35 metros del mismo. la antena de 96 x 90 cm de diametro, estara sobre un soporte o pie de 78 cm de altura, quedando la parte mas baja a (78-(96/2) = 30 cm) . deseamos saber cual sera la elevacion minima que podremos apuntar con esa antena.
recordemos que en este caso,podemos redondear algunos valores, dado que solo necesitamos una aproximacion de 1 grado.
Datos que conocemos:
H = 30 cm
B = 150 cm - H = 120 cm
A = 135 cm
gamma = 90 grados
sen gamma = 1
calculamos el valor del lado C, segun pitagoras: C= SQR (A^2 + B^2) =
C = SQR (135^2 + 120^2) = SQR ( 18225 + 14400) = SQR(32625) = 180,63 tomamos 180 cm
aplicamos el teorema del seno y hacemos:
sen beta = B * sen gamma / C
sen Beta = 120 * 1 / 180 = 0.666...
con este dato vamos a la tabla del seno adjunta en el post y calculamos el valor del angulo aproximado. vemos que el mas cercano es 42 grados, para un valor de 0.669.
entonces:
C = 180 cm
BETA = 42 grados
ALFA = 180 - (90 + 42) = 48 grados
y ya tenemos resuelto el problema. 42 grados es el angulo menor de elevacion real que la antena puede apuntar en estas condiciones de manera perpendicular muro. toda elevacion menor, es impedida por el muro. luego, a medida que giramos la antena a la derecha o la izquierda, la distancia al muro va cambiando,permitiendonos cada vez un angulo menor de elevacion. en ese caso debe recalcularse el mismo.
EL CASO DE UN ARBOL / EDIFICACION DE ALTURA DESCONOCIDA:
veamos que hacer en ese caso, si tenemos un arbolito gigante que justo el vecino ha plantado hace años y se levanta desafiante frente a nuestra antena parabolica, o que quizas esta en nuestro terreno pero ya no estamos como para interpretar el papel de "tarzan de los monos" y treparnos al mismo para conocer su altura. que hacemos entonces ?, recurrimos a las Matematicas.
Sea empleando un transportador y un tubo plastico de unos 30 cm sobre un pie improvisado de alguna camara de fotos o una mesa, o sea con un teodolito profesional, pero de alguna manera tenemos que averiguar el angulo BETA. ese sera nuestro dato fundamental.tratemos de que ese dato tenga una certeza dentro del grado. luego, con la cinta metrica medimos la distancia A, desde el punto de medicion del angulo y hasta el pie del arbol. La idea es valernos del teorema del seno y luego por pitagoras, para resolver rapidamente el problema.
como lo hacemos ?
Sea un arbol situado a una distancia A = 17 metros del punto de medicion, luego armamos un teodolito casero, con un tubo plastico y un transportador de angulos escolar, y con el medimos la copa del arbol, la parte mas alta y nos da 32 grados. el punto de apoyo del medidor casero de angulos esta a 1.2 metros sobre el suelo.
Datos que Conocemos:
H = 1.2 mts
lado A = 17 mts
Angulo BETA = 32 grados
angulo Gamma = 90 grados
angulo ALFA = 180 - (90 + 32) = 58 grados
queremos conocer el valor de B.
sabemos que A/sen alfa = B/sen beta = C/sen gamma
despejamos B = A * sen beta / sen alfa = 17 * (sen 32*)/ (sen 58*)
entonces B = 17 * 0.530 / 0.848 = 10.625 mts
luego el punto de medicion estaba a una altura H, sumamos esa altura a la altura B hallada y nos da el resultado final de la altura del arbol = 10.625 + 1.2 = 11.825 mts
si queremos calcular C, podemos hacerlo, para tener todos los datos, aplicando el teorema de pitagoras, dodne C= SQR (289 + 139.83) = SQR (428,83) = 20,71 mts
Ahora bien, si la parte inferior del plato de la antena se ubicara a 1.2 metros y si en el punto de la medicion se ubicara la antena, estos datos son sirven, pero si la antena va instalada en otro lado, estos calculos que hemos hecho solo nos sirven para conocer la altura del arbol, nada mas.
Ahora sabemos algo que antes no sabiamos: la altura del arbol. y para el proximo calculo, sera mas facil la cuentita.
supongamos que en realidad medimos desde el patio, pero la antena, viendo el angulo de elevacion, decidimos colocarla sobre un poste de 3 metros, un metro mas lejos del arbol y a 2 metros de altura queda la parte mas baja de la antena una vez colocada en el poste.
ahora podemos recalcular para saber cual es el angulo menor de elevacion que podra alcanzar esa antena. variamos el valor de H, el cual ahora vale 2 metros y variamos el valor de A, el cual ahora vale 18 metros.
RECALCULANDO:
conocemos los valores de:
B = 11.825 mts - 2 mts = 9.825 mts
A = 18 mts
H = 2 mts
gamma = 90 grados
sen gamma = 1
sabemos por pitagoras que C = SQR (18 * 18 + 9.825 * 9.825) = SQR(324 + 96.53) = 20.50 mts
sabemos que B/sen beta = C/sen gamma entonces sen beta = B * sen gamma / C = B/C
aplicamos la formulita: sen Beta = 9.825/20.5 = sen 0.45122 = 27 grados.
Desde esta nueva posicion de la antena podremos apuntar a una elevacion minima de 27 grados en la direccion del arbol de 11.825 mts que tiene enfrente a 18 metros.
Espero que estos calculos sean de ayuda, para los ftaperos que tienen obstaculos cerca de su estacion satelital.
Aprovecho para indicar que el MITO de instalar la antena invertida, en los casos en que haya un obstaculo hacia el satelite es, justamente eso, un MITO, una mentira, algo falso, dado que la señal sigue llegando al lnbf en el mismo angulo, aunque la antena parezca apuntar mas hacia arriba. Si un obstaculo impide que la señal llegue a la antena en la posicion usual, tambien le afectara en la posicion invertida. La unica salida para evitar el obstaculo, es ubicar la antena en una nueva posicion desde la cual la señal satelital pueda llegar libremente al plato. La antena se emplea invertida, en satelites de bajo horizonte, por otras cuestiones tecnicas, como el ruido de la antena y el ruido de la tierra, entre otras.
TABLA DEL SENO PARA LOS CALCULOS EXPLICADOS:
pelar la funda exterior 10 mm
con cuidado de no cortar la pantalla
deberia quedar algo asi, se ve la malla y debajo la pantalla
echamos hacia atras los hilos de la malla
despues la pantalla tambien para atras
cortamos el dielectrico a 3 cms del inicio de la malla
nos quedaria asi
enrosco el conector en sentido agujas del reloj
quedaria asi
